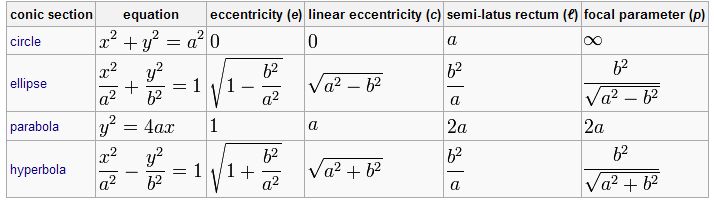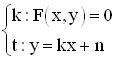Окръжност, елипса, хипербола и
парабола. Допирателни към тях
Окръжност, елипса, хипербола и
парабола. Допирателни към тях

Съдържание.
Бележка от автора. При написването на този учебен материал са използувани съществено илюстрации от световната INTENET енциклопедия, което навсякъде е потвърдено чрез съответните адреси с хипервръзки.
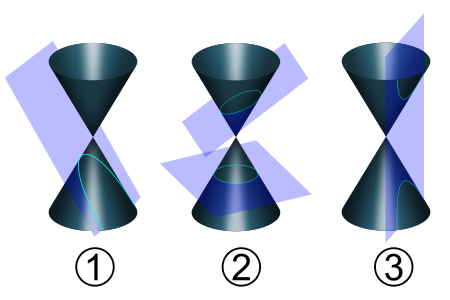
В математиката коничните сечния се дефинират като криви, получени при пресичането на конична повърхнина с равнина.
Коничните сечения могат да бъдат дефинирани и като алгебрични криви от втора степен:
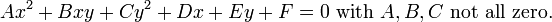
Трета дефиниция (една от най - често срещаната в учебните помагала по аналитична геометрия) е следната: геометрично място на точки в равнината, които притежават свойството: отношението между разстоянието им до дадена точка в същата равнина, наречена фокус, и разстоянието им до дадена права в същата равнина (наречена директриса), е постоянно, наречено ексцентрицитет е.
При 0 < e < 1 коничното сечние се нарича елипса, при e = 1 - парабола, при e > 1 - хипербола. Окръжността се разглежда като частен случай на елипса, като двете са затворени криви, за разлика от остналите 2 вида конични сечния: парабола и хипербола. По - долу показваме с анимиран аплет и още един чертеж общата връзка между 3 вида конични сечения с хипервръзки към световната енциклопедия.
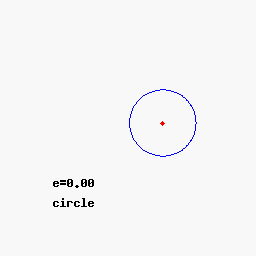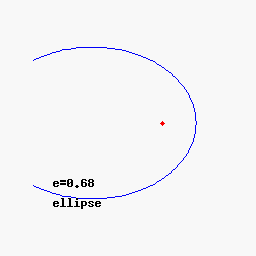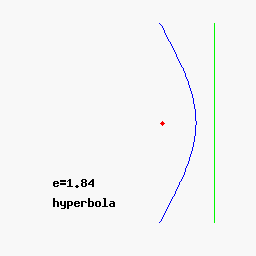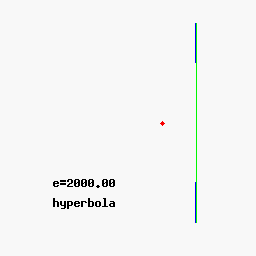
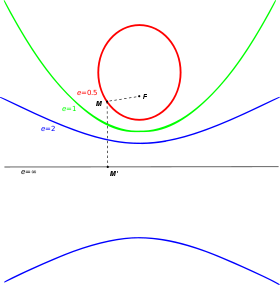
Общо полярно уравнение на коничните сечения.
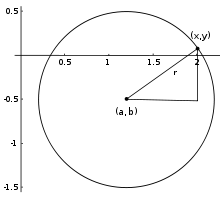
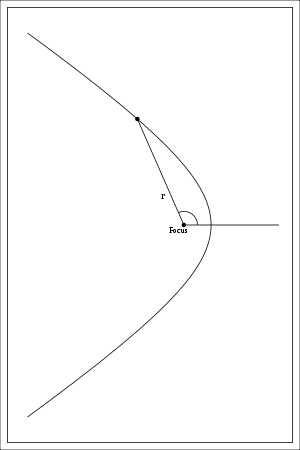
Спрямо полярна координатна система, която е изобразена на фигурата по - долу:
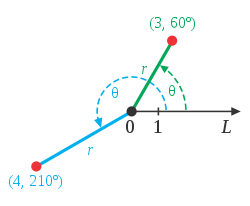
коничните сечния имат общо полярно уравнение: 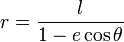 , където:
, където: 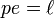 . (p) е разстоянието от фокуса (един или два) до (съответната) директриса. Въвеждаме параметрит (а), (с) с формулите:
. (p) е разстоянието от фокуса (един или два) до (съответната) директриса. Въвеждаме параметрит (а), (с) с формулите: 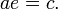 ;
; 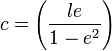 .
.
Канонични уравнения на коничните сечения.След няколко смени на координатната система коничните сечения получават т. н. канонични (най - правилни, най - удобни и кратки) уравнения, които са посочени в първата колона на таблицата по - долу. Обърнете внимание и на следващите колони, особено на колоната, в която е посочена връзката между параметрите а, в, с.
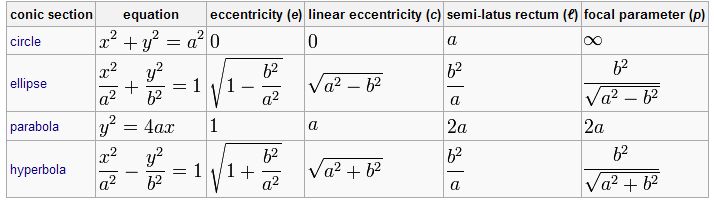
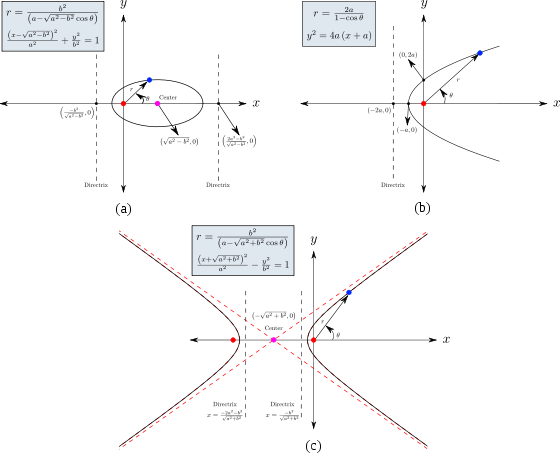
Подробни чертежи за 3 вида конични сечения - на следващите фигури.
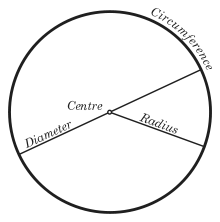
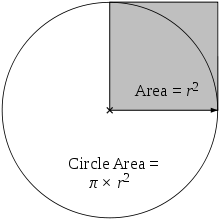
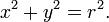
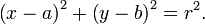
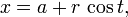
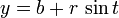
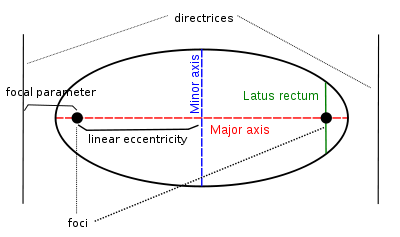
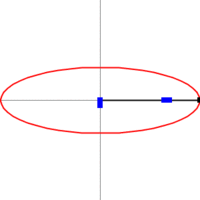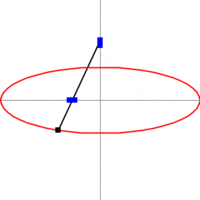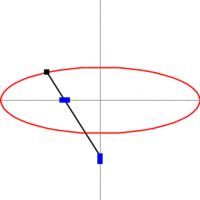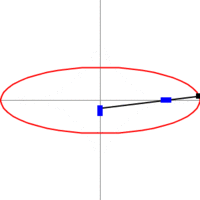
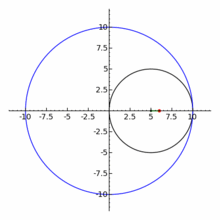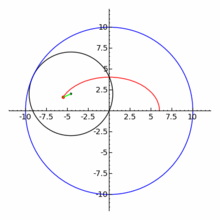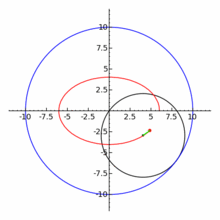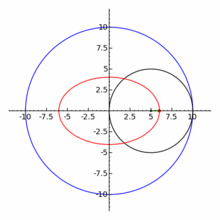
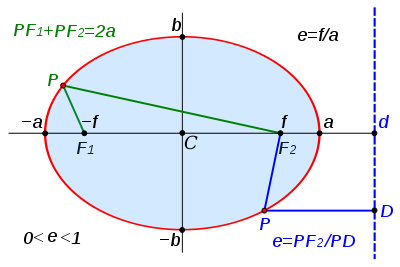
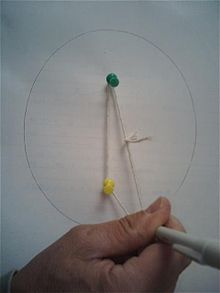
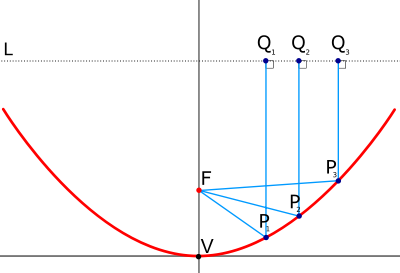
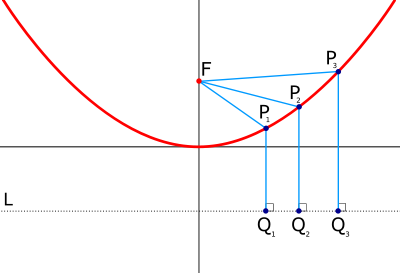
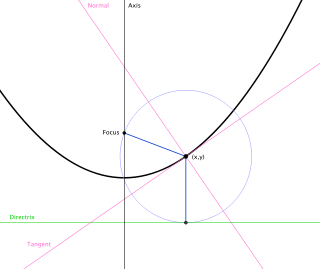
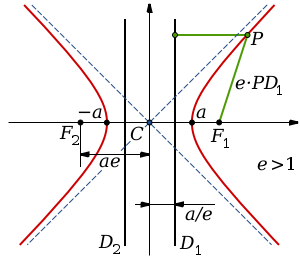
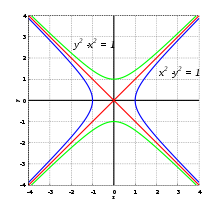
На фигурата по - долу са посочени формите на 3 вида конични сечения, заедно със свързаните с тях формули. Начертани са директрисите и са посочени местата на фокусите. От фигурата има хипервръзка към уголемения й формата световната ИНТЕРНЕТ енциклопедия.
Допирателни към конични сечения.Идея за допирателни към конични сечения. Вече видяхме, че едно конично сечение се представя като уравнение на алгебрична крива от втора степен. Тангентата (допирателната) към него е права, която има само една обща точка с него. Следователно, въпросът се свежда до намиране на достатъчни условия системата от 2 уравнения с две неизвестни, записана по - долу, да има едно двойно решение.
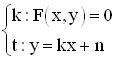
От второто уравнение заместваме стойността на втората променлива в първото уравнение на даденото конично сечение. Получаваме алгебрично уравнение от втора степен. За да има двоен корен, анулираме дискриминаната му, с което осигуряваме зависимост между 2 параметъра в уравнението на тангентата. Обикновено в условията на задачата са поставени допълнителни изисквания към допирателната, които спомагат за нейното конкретизиране.
 Окръжност, елипса, хипербола и
парабола. Допирателни към тях
Окръжност, елипса, хипербола и
парабола. Допирателни към тях![]()
![]()




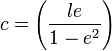 .
.